Quantum computing is here, and it’s on the cloud. As someone who loves both quantum computing and the cloud, this makes me very happy. I did a doctorate in quantum computing in the late 1990s. By necessity, my research was purely theoretical. We knew quantum computers would be powerful, but no one had actually built one. The big question for our watercooler debates wasn’t “when will a quantum computer be built?” it was “will a quantum computer ever be built?”.
Things have changed. In 2016 IBM was the first to make a quantum computer available on the cloud - for anyone to use, for free. Progress has continued since then, and a developer can now run quantum workloads on a number of different clouds. They can develop their cloud-ready quantum applications using a variety of open source or proprietary quantum libraries and compilers. The cloud is a natural fit for quantum computation, because the cloud is just so good at pooling resources, enabling hardware access, and accelerating innovation. Practical quantum computation takes a hybrid approach in which quantum and classical hardware work in concert. The two different types of system each pick up the parts of the problem they’re best at. Cloud Native technologies, like Kubernetes, will be a fundamental part of this orchestration.

Why would someone want a quantum computer?
Quantum computers are interesting because classical computers are limited. Some problems are just too difficult to work out on a classical computer. I don’t mean things like designing an auto-correct that doesn’t make bizarre changes or teaching a computer to tell jokes. Those are hard, but that’s just because we can’t figure out the right algorithm. But for some problems, we do know the algorithm, and it’s still too hard: even the most efficient algorithm takes so much time and memory that it’s physically impossible to run. The underlying issue is that the algorithm scales exponentially with the number of things in the calculation.
Oddly, these intractable problems often seem easy. For example, imagine trying to work out an optimum seating plan for some dysfunctional colleagues. If you sit them near someone they don’t like, they’ll kick each other’s shins or lob paperclips across the table. If there’s real hatred, they’ll pour tea into one other’s keyboards. (If this is actually your team, stop reading this article and go read up on psychological safety instead.) Your aim is to minimise disruption by coming up with a seating plan that somehow keeps the peace.
If there are two people in the meeting, the calculation is easy - there are only two combinations to try. Bob can be on Alice’s left, or Bob can be on Alice’s right. With five people, we have to try out 120 combinations. Should Bob be on Alice’s right with Eve in the middle and Clive on the end and Darcy opposite Bob? Or maybe Bob and Eve is such a bad combination that we put Clive in between them and Eve on the end, or … ?
 With twenty colleagues, we need to try a quintillion combinations to find the best one. That’s hard.
With twenty colleagues, we need to try a quintillion combinations to find the best one. That’s hard.
The angry-colleague-seating-plan is (hopefully) a bit unrealistic, but many actually-important problems scale in a similarly challenging way. For example, even the largest supercomputers can only accurately simulate molecules with a few dozen atoms. The problem gets hard fast because every atom in the molecule interacts with every other atom. Accurately simulating a relatively simple molecule like caffeine would need 10^48 bits of memory. That sounds big, and it is - it’s about 10% of the number of atoms in the earth.
These sorts of problems are everywhere, in almost every domain. Balancing risk in a portfolio is a bit like the angry colleague problem, except with investments instead of grumpy people. Transaction settlement in a trading system or working out the optimum route between cities for a logistics company are also computationally complex. They’re easy for a small number of cities or trading partners, but intractable when the numbers get large.
Now we get to the quantum. Quantum computers are interesting because they can solve some of these problems far more efficiently. Instead of scaling exponentially, the difficulty scales linearly or quadratically with the number of participants. That change in scaling turns the basically-impossible into “possible, if we can build a biggish quantum computer”.
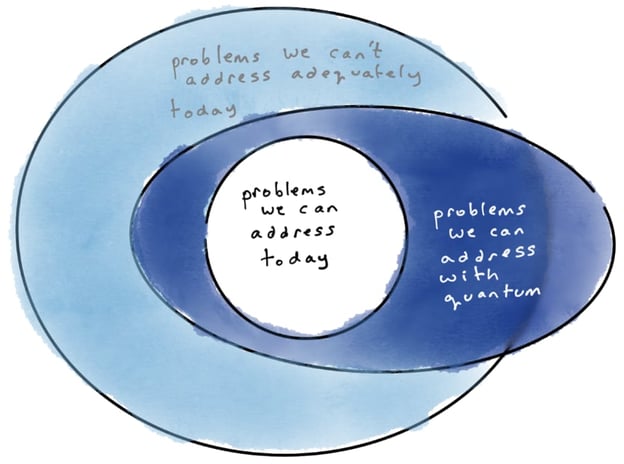
Some problems, like multiplying two huge numbers or streaming videos, are quick to do on a classical computer (white area). Other problems, like finding the factors of a huge number or simulating a complex molecule, are very hard to do on a classical computer, no matter how big the computer (light blue area). Some - but not all - of these hard problems can be quickly solved on a big quantum computer. Quantum computers may even be able to address future problems beyond what we now know.
It’s important to note that quantum computers are only faster for certain kinds of problems. A quantum computer isn’t just a really fast computer or a magic computer that’s better at everything. It’s a computer that operates by different rules, and those rules are sometimes - but not always - helpful.
Qubits, bits, and entanglement
All computers store and manipulate information. Today’s classical computers manipulate individual bits, which store information as binary 0 and 1 states. Once you have millions of bits, you can do useful things like sharing cat memes on social media or giving communities early warning about earthquakes.
Quantum computers are different - except for the cat part, but we’ll come back to that. Quantum computers store information differently from classical computers, and they manipulate it differently. Instead of normal bits, quantum computers rely on quantum bits, or qubits. A classical bit can only be 0 or 1, but a qubit can be in a combination of states, known as a superposition.
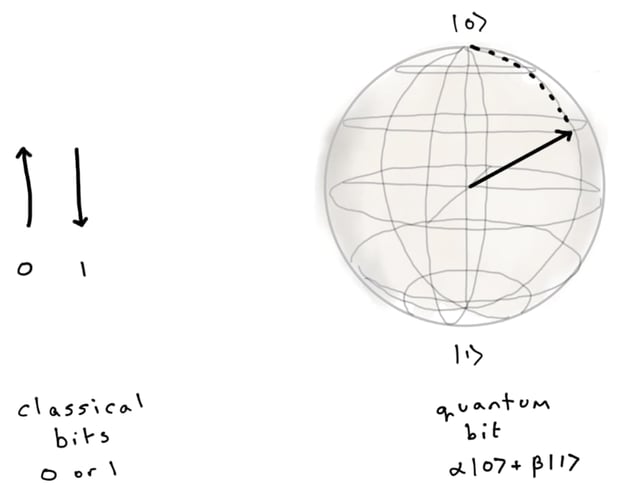
If we represent bits as vectors, a classical bit only has two possibilities: pointing straight up (0) or straight down (1). A qubit has any number of possible combinations of |0⟩ and |1⟩ . The combination has a phase, which is why we represent it as a sphere and not a circle.
What happens when we measure a qubit? Measurement is a classical operation, so the qubit collapses to either |0⟩ or |1⟩ , allowing us to read out an answer that we, and our classical computers, can understand. If the qubit was a combination of |0⟩ and |1⟩ states when we measured it, there’s an element of chance in whether we get a 0 or 1. If the qubit is a 50-50 mix of |0⟩ and |1⟩ , the result of our measurement is perfectly random. If, on the other hand, the state was mostly |1⟩ , we’re very likely to read out a 1.
In addition, classical bits are physically independent of each other, but qubits can be entangled with one another. Entanglement means the states of qubits are correlated in a way that can’t be replicated classically. For example, imagine a logic gate between two qubits in which the second bit is flipped only if the first, control, bit is |1⟩ . If the control bit is a vanilla |0⟩, the second bit isn’t flipped. If it’s a vanilla |1⟩ , the second bit is flipped. But what if the control bit is a mix of |0⟩ and |1⟩ ? The second bit is now also a mix of |0⟩ and |1⟩ , but it’s not an arbitrary mix.
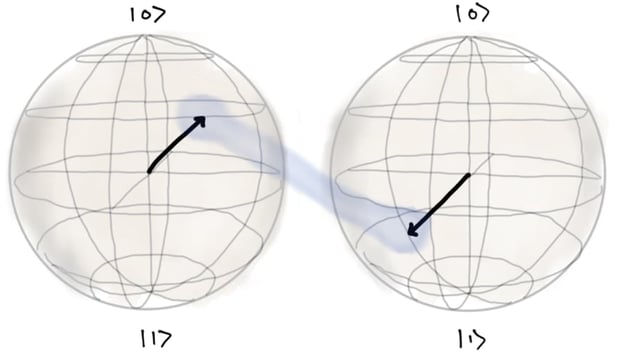
Visualising entanglement is hard. That’s partly because we just don’t have a good classical analogy for what’s going on.

As Einstein, Schrödinger and Bohr wrestled with the implications of the new quantum theories at the beginning of the last century, I imagine they said the scientific equivalent of “WTF?”. Schrödinger devised his cat paradox to show how absurd some of the new quantum theories seemed. If a particle which is a mix of |0⟩ and |1⟩ interacts with a larger system, would that system itself become a mix of states, until it’s measured? For example, if a cat is shut in a box and release of a cat-killing-poison is triggered by the state of a single qubit which is in a superposition of |0⟩ and |1⟩ , is the cat in a superposition of alive and dead until someone opens the box and measures the cat? You’ll be relieved to know the answer is “no” - as the qubit interacts with the larger system, it loses its ‘quantumness’. This process is known as decoherence.
This is where things get extra-fun. If two qubits are entangled, measuring one qubit pre-determines the answer we get when we measure the other qubit. This happens even when the two qubits are too far away to influence each other. Each qubit, individually, will behave randomly, but the answers we get when we measure them are strongly correlated. Going back to our two qubits, if the first qubit is measured and yields a |0⟩, we know the second qubit will be a |0⟩. If the first qubit yields |1⟩ , the second qubit has to be a |1⟩ . Even though the measurement result of each qubit is random, we will never get a situation where we measure |1⟩ and |0⟩ or |0⟩ and |1⟩ . This means we can’t represent the state of the second qubit without also including the first qubit.

The best-known analogy for quantum entanglement involves observation of mismatched socks. We’re here for the computers, not the sock philosophy, so I won’t go into the details, apart from observing that leading quantum physicists have concluded that entanglement is more mysterious than odd socks.
Algorithms
Is it useful to measure a qubit and get a random number? Unless you’re trying to make a really great random number generator, no. What most quantum algorithms do is try to manipulate the system into a state where each qubit is mostly |0⟩ or mostly |1⟩ , so that when everything is measured there’s a high probability of getting the right answer.
Most algorithms work by creating a superposition of lots of different possible solutions and then interfering the different quantum states together so that the correct answers are amplified and the wrong answers cancel each other out. ‘Interfering answers’ isn’t something that makes sense for a classical computer, but quantum systems act a bit like waves. This is called wave-particle duality, and, even physicists agree that it’s counter-intuitive.
Interfering different answers together to make some answers disappear is a bit like how noise cancelling headphones use differently-phased noise to cancel out unwanted noise, except that the thing being cancelled out is a number which isn’t a factor of 2971215073, rather than airplane noise. If you’re thinking that sounds tricky to achieve, you’re not wrong. There are a relatively small number of quantum-native algorithms - that is, algorithms which take full advantage of the quantum characteristics of a quantum computer.
These algorithms have the potential to be much much faster than the fastest equivalent classical algorithm. For small-scale problems, the quantum speed-up may not be noticeable, or may even be outweighed by the slower rate at which quantum processors perform operations. When the problems get bigger though, the scaling behaviour matters a lot.
The best problems to have
Where will quantum computers be most useful? Quantum applications fall into three general categories:
- Simulating quantum systems
- Artificial intelligence
- Optimisation and Monte Carlo
Chemical simulation was the first proposed use case for a quantum computer, and it’s potentially very valuable. Quantum systems (like molecules) are too complex to accurately model classically, but a quantum computer has the same quantum-ness so it can cope with the complexity. For example, exploring possible materials on a quantum computer might allow us to discover new battery technologies or drugs.
Quantum artificial intelligence is a growing area. Quantum computers will be useful for better model training, pattern recognition, and fraud detection.
Finally, optimisation problems are a good fit for quantum algorithms. For example, Monte Carlo simulations are known to be faster on a quantum computer. These types of algorithms are widely used in financial applications like portfolio optimisation, risk analysis, and credit scoring.
The future of Schrödinger’s cat
My employer, IBM, doesn’t feature a single cat in their quantum tutorials, nor do the other quantum vendors. In a way, this isn’t surprising - the future of quantum computing is as a tool for solving hard, valuable, business problems, not a cat-themed intellectual curiosity. Are we there yet? Not quite.
At the moment, quantum computers are real, but they’re small. Every problem that we can currently solve on a quantum computer could also be solved on a classical computer. We’re working towards quantum advantage, which is when quantum computers will be able to answer questions that a classical computer couldn’t.
The path towards quantum advantage is promising. For example, IBM’s quantum roadmap includes putting a 1,121 qubit quantum computer online in 2023. That’s enough qubits to enable quantum advantage. The number of qubits is important, but also important is the robustness of the qubits. “Quantum volume” is an important metric which combines the number of qubits and their quality. Much hardware research in quantum computers is focussed on reducing error rates and increasing how long it takes for a system to decohere, to increase the quantum volume of a system. Researchers are also working to reduce the physical size of the chips, connect more of the system together in integrated units, and, because quantum computers need to be kept ridiculously cold, make really great fridges.
As well as physical error reduction, software error correction is possible. Classical computers do error correction at the bit level by grouping physical bits into logical bits and taking a majority vote. In the quantum case, doing a simple majority vote doesn’t work; voting mid-calculation would mean measuring the qubits mid-calculation, and that would collapse everything to |0⟩ or |1⟩ . Nonetheless, clever algorithms do exist which can group physical qubits into error-corrected ‘logical’ qubits and do majority votes without actually voting. 1,121 physical qubits is enough qubits to implement error correction and come out with enough logical qubits to do useful computations.
Abstraction
At the moment, if you learn quantum computing, you usually start with the principles of quantum mechanics, and then move on to quantum gates. You might also learn about superconductors and fridges and other physical implementation details. Once you’ve got a handle on gates, you might read up on the workings of notable algorithms like Shor and Grover.
This isn’t how most of us learn to program classical computers. Normal computers don’t excite us because there are bits and algorithms inside, they excite us because we can use them to program games and sell things and automate away boring tasks. As programmers, we may start with hello world, but we quickly move on to programming our own hot dog recognition service or autonomous ship. I think we’re going to get to the same point with quantum computers, and I think it’s going to happen quickly.
Already, quantum libraries are moving up the stack. For example, some parts of qiskit allow you to work at the level of individual qubits and gates, but there’s a growing set of domain-specific libraries for finance, machine learning, chemistry, physics, and optimisation. These libraries will become increasingly frictionless. Eventually users might not even know (or care) if a program is running in a quantum or classical way under the covers.

Frictionless. Bad for cats, good for developers.
Hybrid Cloud
Quantum computers are (so far) very large, and very very cold. They’re fantastic for certain categories of problems, but not for all problems. Even where a quantum algorithm is the best way of solving a problem, it works in concert with a classical ‘support algorithm’ to store large values, hold intermediate results, and pipeline different stages of an algorithm.

As quantum computers increase in power, the role of the support computer may get smaller, but it’s not going to go away. Because they’re so specialised, lifting and shifting classical operations to quantum computers just isn’t a great idea. Instead, hybrid systems will use orchestration to route different parts of a problem to the optimum hardware. At least some of that orchestration will be baked into familiar platforms such as Kubernetes.
Why cloud?
Quantum computation is a natural fit for the cloud. Although the chips are small, the computers themselves are big. Some of the extra space is supporting electronics and control circuits, but most of the bulk is a great big refrigerator.
This is because, to keep them stable and reduce interference with the outside environment, quantum computers need to be kept cold. Very cold. Most quantum computers operate at a few thousands of a degree above absolute zero. IBM’s computer is kept at -273.1 °C, colder than the space between the stars.
For the moment, as they get more qubits, quantum computers are also getting physically bigger. IBM is planning to make a 10’ high and 6’ diameter ‘super-fridge’ to keep its 1,121 qubit computer cold. The generation of computers after that may involve multiple super-fridges connected together. That’s the kind of thing which is great ... in someone else’s data center.
Quantum computers represent an extraordinary feat of engineering, both in the refrigeration, but also in the electronics, materials design, and control logic. It’s not easy or cheap to build a quantum computer, and at the moment, there are only a small number of quantum computers in the world. It’s a bit like the early days of classical computing, but with one big difference – access. The cloud is great for pooling resources, so the number of people who’ve executed a program on a quantum computer is much higher than it was at a similar point in the evolution of classical computers.
This easy access to the infrastructure is complemented by a thriving open source community on the software side. Broad, cloud-based access to these marvellous machines, supported by an open source ecosystem, is making the next generation of computing.



 Previous article
Previous article
